To complete the square, equations with an x squared coefficient of 1 should be written in this form:

To complete the square, the x coefficient has to be divided by two. This value would then become the value of p. The value of p has to then be squared and multiplied by -1. This value has to then be added or subtracted from the constant.
Consider this example:
In addition to this, equations with an x squared coefficient not 1 should be written in this form:
The coefficient of x squared has to be divided by the x squared coefficient as well as the x coefficient. Then the square can be completed.
An example is shown below.
Solving equations by completing the square
To solve equations by completing the square, the value of x has to be isolated, or left on its own.
Consider this, from the previous example:
Finding minimum and maximum points by completing the square
The value of x in the completed square which makes the equation in the bracket equal 0 is the x-coordinate of the point, and the value of y is the value of the constant. For example, the minimum point of the second equation is (-2, -13).



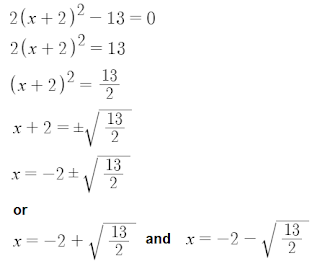
No comments:
Post a Comment